Контрольні запитання
1. Що таке важіль?
Важіль — це тверде тіло, яке може обертатися навколо нерухомої осі (точки опори).
2. Наведіть приклади застосування важеля.
Ножиці, гойдалка, лом, ваги, щипці, гайковий ключ.
3. Дайте означення плеча сили.
Плече сили — це відстань від осі обертання (точки опори) до лінії дії сили.
4. Якою рівністю записують правило важеля?
$$ F_1 \cdot d_1 = F_2 \cdot d_2 $$
де $ F_1 $ і $ F_2 $ — сили, $ d_1 $ і $ d_2 $ — їхні плечі.
5. Дайте означення моменту сили.
Момент сили — це фізична величина, що дорівнює добутку сили на її плече:
$$ M = F \cdot d $$.
6. Якою є одиниця моменту сили в СІ?
Одиниця моменту сили в СІ — ньютон-метр (Н·м).
7. Сформулюйте правило моментів
Для рівноваги важеля сума моментів сил, що обертають важіль в один бік, дорівнює сумі моментів сил, що обертають його у протилежний бік.
8. Чи завжди важіль застосовують для отримання виграшу в силі? Наведіть приклади
Не завжди. Наприклад, у щипцях важіль використовують для виграшу у відстані, а не лише у силі. Чи весла човна – щоб досягти високої частоти гребків і швидкого руху.
Вправа 2
1. Маса якої людини на рис. 1 є більшою? Поясніть свою відповідь.
Відповідь:
Маса хлопчика (праворуч) є більшою.
Пояснення:
Гойдалка — це класичний приклад важеля, який перебуває у рівновазі, коли виконується умова:
$$ F_1 \cdot d_1 = F_2 \cdot d_2 $$
де:
- $F_1$ і $F_2$ — сили тяжіння (вага) людей,
- $d_1$ і $d_2$ — відповідні плечі (відстані від осі обертання до місця, де сидить кожна людина).
На рисунку видно, що дівчинка (ліворуч) сидить далі від осі обертання, а хлопчик — ближче. Оскільки важіль у рівновазі, то людина, яка сидить ближче до осі (хлопчик), має більшу масу, ніж та, що сидить далі (дівчинка). Це випливає з умови рівноваги важеля: якщо плече менше, то сила (тобто маса) має бути більшою, щоб моменти сил зрівноважувалися.
2. Розгляньте рис. 2. Який важіль застосовують для виграшу в силі, а який — для виграшу у відстані? Відповідь обгрунтуйте.
Весло використовується для виграшу у відстані. Точка опори (місце кріплення весла до човна) знаходиться між точкою прикладання сили (руками весляра) та точкою, де весло діє на воду. У цьому випадку $d_1 < d_2$, де $d_1$ — плече прикладеної сили, а $d_2$ — плече сили, що діє на воду. Це дозволяє човну пропливати більшу відстань при кожному гребку, але вимагає більших зусиль.
Молоток-цвяходер використовується для виграшу в силі. Точка опори (місце контакту молотка з поверхнею, з якої витягується цвях) знаходиться між точкою прикладання сили (рукою) та точкою, де молоток діє на цвях. У цьому випадку $d_1 < d_2$, де $d_2$ — плече прикладеної сили, а $d_2$ — плече сили, що діє на цвях. Це дозволяє витягувати цвяхи з меншими зусиллями.
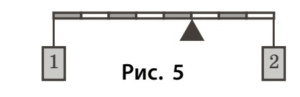
Задача 3
Умова: Вага вантажу 1 становить 90 Н (рис. 3). Визначте вагу вантажу 2.
Дано:
- $F_1 = 90 \text{ Н}$
- $d_1$ = 3 поділки
- $d_2$ = 5 поділок
Знайти: $F_2 = ?$
Розв’язання:
За правилом важеля:
$$ F_1 \cdot d_1 = F_2 \cdot d_2 $$
$$ F_2 = F_1 \cdot \dfrac{d_1}{d_2} = 90 \text{ Н} \cdot \dfrac{3}{5} = 54 \text{ Н} $$
Відповідь: Вага вантажу 2 становить $54 \text{ Н}$.
Задача 4
Умова: Визначте масу вантажу (рис. 4), якщо на правий кінець важеля діє сила $40 \text{ Н}$.
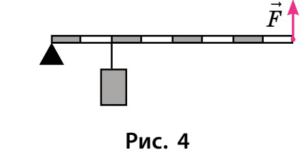
Дано:
- $F = 40 \text{ Н}$ (на правому кінці)
- Вантаж підвішено на відстані $d_1 = 2$ поділка від опори, сила $F$ діє на відстані $d_2 = 8$ поділок.
Знайти: $m = ?$
Розв’язання:
За правилом важеля:
$$ F_1 \cdot d_1 = F_2 \cdot d_2 $$
$$mg d_1 = F_2 d_2$$
Підставимо значення (приймаючи $g \approx 10$ Н/кг):
$$m \cdot 10 \cdot 2 = 40 \cdot 8$$
$$m \cdot 20 = 320$$
$$m = \dfrac{320}{20} = 16 кг$$
Відповідь: маса вантажу становить 16 кг.
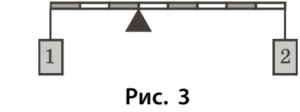
Задача 5
Умова: Загальна маса вантажів на рис. 5 — $48 \text{ кг}$. Визначте масу кожного вантажу.
Дано:
- $m_1 + m_2 = 48 \text{ кг}$
- Плечі: $d_1 = 5$, $d_2 = 3$ (умовні поділки).
Знайти: $m_1 = ?$, $m_2 = ?$
Розв’язання:
За правилом важеля:
$$ m_1 \cdot d_1 = m_2 \cdot d_2 $$
$$ m_1 \cdot 5 = m_2 \cdot 3 $$
$$ m_1 = \dfrac{3}{5} m_2 $$
$$ m_1 + m_2 = 48 $$
Підставимо $m_1$:
$$ \dfrac{3}{5} m_2 + m_2 = 48 $$
$$ \dfrac{8}{5} m_2 = 48 $$
$$ m_2 = 48 \cdot \dfrac{5}{8} = 30 \text{ кг} $$
$$ m_1 = 48 – 30 = 18 \text{ кг} $$
Відповідь: Маса першого вантажу — $18 \text{ кг}$, другого — $30 \text{ кг}$.
Задача 6
Умова: До кінців тонкого однорідного стрижня завдовжки $2 \text{ м}$ підвішено вантажі масами $14$ і $26 \text{ кг}$. На якій відстані від середини стрижня слід розмістити опору, щоб стрижень перебував у рівновазі?
Дано:
- $L = 2 \text{ м}$
- $m_1 = 14 \text{ кг}$ (лівий кінець)
- $m_2 = 26 \text{ кг}$ (правий кінець)
Знайти: $x = ?$ (відстань від середини до опори)
Розв’язання:
Нехай опора розташована на відстані $x$ праворуч від середини.
Відстань від опори до $m_1$: $d_1 = 1 + x$ Відстань від опори до $m_2$: $d_2 = 1 – x$
За правилом важеля:
$$ m_1 \cdot d_1 = m_2 \cdot d_2 $$
$$ 14 \cdot (1 + x) = 26 \cdot (1 – x) $$
$$ 14 + 14x = 26 – 26x $$
$$ 14x + 26x = 26 – 14 $$
$$ 40x = 12 $$
$$ x = 0{,}3 \text{ м} $$
Відповідь: Опору слід розмістити на $0{,}3 \text{ м}$ (30 см) праворуч від середини стрижня.
Завдання 7
Розгляньте рис. 6 і поясніть: чому ножиці для різання металу мають довгі ручки, а для різання тканини — короткі; як «працює» гайковий ключ; яким ключем легше відкрутити гайку — з довгою ручкою чи з короткою.

Відповідь:
- Ножиці для металу мають довгі ручки, бо чим більше плече сили, тим більший момент сили створюється при тій самій силі. Це дає виграш у силі — легше різати тверді матеріали. Для тканини таких зусиль не потрібно, тому ручки короткі й завдяки цьому швидше ріже.
- Гайковий ключ — це важіль: чим довша ручка, тим більший момент сили можна створити, прикладаючи ту ж силу.
- Легше відкрутити гайку ключем із довгою ручкою, бо при більшому плечі потрібна менша сила для того самого моменту сили.
Задача 8
Умова: Маса вантажу 1 — $10 \text{ кг}$, вантажу 2 — $5 \text{ кг}$ (рис. 7). Визначте масу вантажу 3. З якою силою важіль тисне на опору?
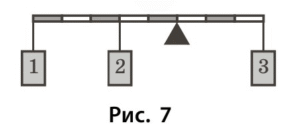
Дано:
- $m_1 = 10 \text{ кг}$ (лівий кінець)
- $m_2 = 5 \text{ кг}$ (середина)
- $m_3 = ?$ (правий кінець)
- Плечі: $d_1 = 5$, $d_2 = 2$, $d_3 = 3$ (від опори)
Знайти: $m_3 = ?$ $N = ?$ (сила тиску на опору)
Розв’язання:
Застосуємо правило моментів (умову рівноваги важеля):
Сума моментів сил, які обертають важіль проти годинникової стрілки, дорівнює сумі моментів сил, які обертають його за годинниковою стрілкою:
$$ m_1 d_1 + m_2 d_2 = m_3 d_3 $$
Підставимо значення:
$$ 10 \cdot 5 + 5 \cdot 2 = m_3 \cdot 3 $$
$$ 50 + 10 = 3 m_3 $$
$$ 60 = 3 m_3 $$
$$ m_3 = \dfrac{60}{3} = 20 \text{ кг} $$
Визначаємо силу тиску важеля на опору ($N$):
Сила тиску дорівнює сумі ваг усіх вантажів:
$$ N = (m_1 + m_2 + m_3) \cdot g $$
Підставляємо знайдені значення:
$$ N = (10 + 5 + 20) \cdot 10 = 35 \cdot 10 = 350 \text{ Н} $$
Відповідь:
$$ m_3 = 20 \text{ кг} $$
$$ N = 350 \text{ Н} $$
Задача 9
Умова: Розв’яжіть задачу, розглянуту в § 2, урахувавши, що маса важеля — $500 \text{ г}$.
Дано: (Задача з §2: $m_2 = 4 \text{ кг}$, $d_1 = 5a$, $d_2 = 3a$; тепер маса важеля $m_{важ} = 0{,}5 \text{ кг}$)
Знайти: $m_1 = ?$
Розв’язання:
Застосуємо правило моментів, враховуючи вагу самого важеля. Момент сили ваги важеля ($M_в$) діє в тому ж напрямку, що й момент сили вантажу 1 ($M_1$).
Умовою рівноваги буде рівність суми цих моментів моменту сили вантажу 2 ($M_2$):
$$ M_1 + M_в = M_2 $$
Оскільки момент сили $M = mgd$, а плече сили тяжіння важеля $d_в = 5a – 4a = a$, маємо:
$$ m_1gd_1 + m_вgd_в = m_2gd_2 $$
Скоротивши на $g$, отримаємо:
$$ m_1d_1 + m_вd_в = m_2d_2 $$
Звідси:
$$ m_1 = \dfrac{m_2d_2 – m_вd_в}{d_1} $$
Визначимо значення шуканої величини:
$$ m_1 = \dfrac{4 \cdot 3a – 0.5 \cdot a}{5a} = \dfrac{(12 – 0.5)a}{5a} = \dfrac{11.5}{5} = 2.3 \text{ кг}$$
Відповідь: $m_1 = 2.3 \text{ кг}$.
Задача 10
Умова: Знайдіть відомості про важелі в тілі людини (див. рис. 8). Складіть задачу за цими відомостями й розв’яжіть її.
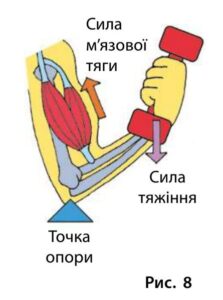
Відомості: У тілі людини кістки та м’язи утворюють важелі. Наприклад, при згинанні руки в лікті точка опори — лікоть, сила м’язової тяги прикладається близько до опори, а сила тяжіння — далі.
Задача: М’яз прикріплений на відстані $d_1 = 4 \text{ см}$ від ліктя, а вантаж тримається на відстані $d_2 = 32 \text{ см}$. Маса вантажу — $5 \text{ кг}$. Яку силу має розвивати м’яз для утримання вантажу?
Дано:
- $d_1 = 0{,}04 \text{ м}$
- $d_2 = 0{,}32 \text{ м}$
- $m = 5 \text{ кг}$
Знайти: $F_{м’яз} = ?$
Розв’язання:
$$ F_{м’яз} \cdot d_1 = m g \cdot d_2 $$
$$ F_{м’яз} = \dfrac{m g \cdot d_2}{d_1} $$
$$ F_{м’яз} = \dfrac{5 \cdot 9{,}8 \cdot 0{,}32}{0{,}04} = \dfrac{15{,}68}{0{,}04} = 392 \text{ Н} $$
Відповідь: М’яз має розвивати силу $392 \text{ Н}$ для утримання вантажу $5 \text{ кг}$ на відстані $32 \text{ см}$ від ліктя.